1. 그래프 G = (V, E)
| V(정점) | 정점: 결합할 객체를 나타냅니다. |
| E(가장자리) | 에지: 연결된 정점 쌍. |
차트란 무엇입니까?
연결된 요소 간의 관계를 표현하는 데이터 구조
즉, 거친 모서리 세트
2. 차트의 종류
| 유형 | 설명 |
| 무방향 그래프 | 트렁크 방향 하지 않았다 그래프 = (i,j) 및 (j,i)는 동일한 에지를 나타냅니다. |
| 유향 그래프 | 트렁크 방향 있다 그래픽 = 나 → 제 = 로 표현 |
| 전체 그래픽 | 한 정점에서 다른 모든 정점으로 연결 최대 모서리 수그래픽 |
| 하위 그래프 | 원본 그래프에서 일부 꼭지점이나 가장자리를 제외하여 만든 그래프 |
| 체중 차트 | 주요 노선에서 무게주어진 그래픽 |
◆ 완전한 그래프 – 에지 수 ◆
무향 그래프 = n(n-1)/2
무향 그래프는 두 정점 사이에 하나의 간선만 가질 수 있습니다.
그러나 유향 그래프는 두 정점 사이에 두 개의 간선이 있기 때문에 무향 그래프의 두 배 크기입니다.
방향 그래프 = n(n-1)
3. 그래프 용어
- 두 꼭짓점 i와 j 사이에 연결된 모서리(i,j)가 있으면 i와 j는 인접한되었습니다
- 이때 에지는 (i,j)입니다. 두 모서리 i와 j에서 사건되었습니다
- 꼭지점
- 머리: 화살촉이 위치한 정점
- 꼬리 : 화살의 꼬리가 있는 꼭지점
- i → j이면 i는 꼬리 볏이고 j는 머리 볏입니다.
- 도 : 꼭짓점에 붙은 모서리의 개수
- In-degree: 꼭지점 방향 모서리의 수
- Out Degree: 정점이 꼬리인 가장자리의 수
- 방향 그래프에서 노드의 차수 = In-degree + Out-degree
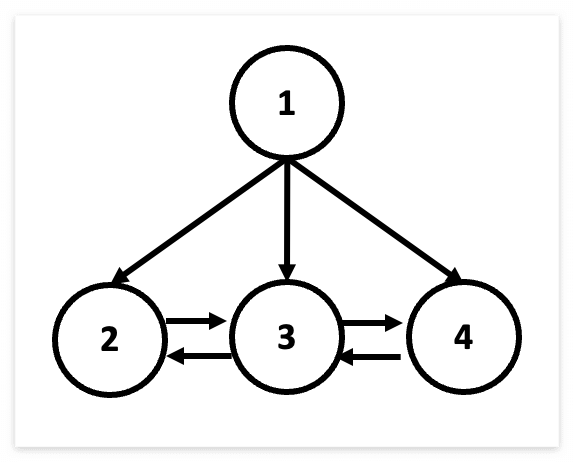
팁 2~에서 순서대로 = 2, 선주문 = 1, 도 = 2+1 = 3
- 떨어져 있는 : 가장자리를 따를 수 있는 일련의 경로
- 경로 길이: 경로를 형성하는 가장자리 수
- 단순 경로: 모든 다른 정점으로 구성된 경로입니다.
- 주기 : 단순경로 중 시작노드와 끝노드가 같은 경로
- 방향성 비순환 그래프(DAG) : 유향 그래프이지만 회로가 없는 그래프
- 그래프에서 두 꼭지점 i, j까지의 경로가 있다면 그것은 꼭지점 i, j이다. 연결된되었습니다
- 연결된 그래프 : 각 정점 쌍 사이의 경로가 있는 그래프
즉, 정점이 제거되지 않은 그래프입니다. - 별도의 그래프 : 정점이 연결되지 않은 그래프
- 연결된 그래프 : 각 정점 쌍 사이의 경로가 있는 그래프